Tensor Networks

Questions

• How can we model quantum systems when there are too many degrees of freedom to even store on a computer?
• How can we use local tensor networks (e.g. matrix product states) to study systems that are, by their very nature, poorly-modeled by local tensor networks?
• Can matrix product state techniques be efficiently extended to two-dimensional problems?

Tensor networks and quantum mechanics

A tensor network usually refers to a decomposition of a high-rank tensor into the product of a bunch of lower-rank tensors. If this decomposition has some regular structure, then we might refer to it as a network. High-ranking tensors can always be broken down like this, but the usefulness of this procedure (from a computational perspective) really comes from the ability to perform approximate decompositions. That is to say, we almost always want to construct tensor networks that keep only the ``most important” information from the original high-rank tensor. This allows us to store and manipulate the tensor network on a computer much more efficiently than the original tensor. The idea behind this is closely related to image compression.

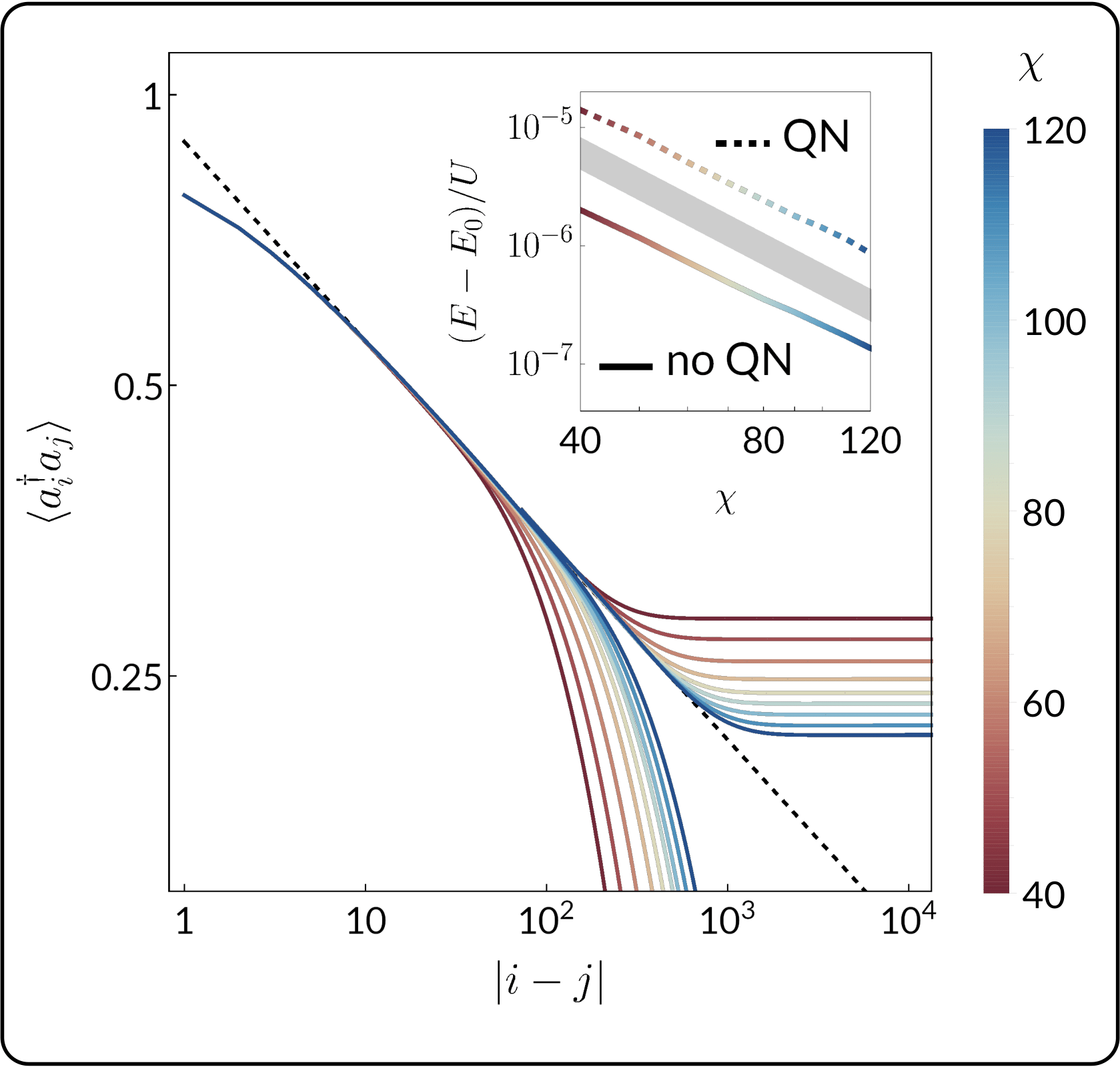
So what does this have to do with quantum mechanics? It turns out that the quantum wavefunction for discrete systems (i.e. systems on a lattice, where particles or spins can only sit on particular sites) can be re-cast as a high-rank tensor, where the tensor rank is equal to the number of physical sites. One can then perform an approximate decomposition of that tensor into the product of local tensors – one for each physical site. In general, this kind of a decomposition (which is local in real space) creates a tensor network known as a projected entangled pair state (PEPS). In one spatial dimension, the PEPS state is referred to as a matrix product state (MPS). This one-dimensional tensor network has a plethora of particularly nice properties, and a suite of tools have been developed in recent years to optimize and time-evolve them, among other things.

In my work, I’ve focused on applying MPS techniques in the thermodynamic limit (i.e. for infinitely-long 1D systems). In particular, I have explored the interplay of spontaneous symmetry breaking with the constraints of tensor network decompositions, which led to a range of practical considerations for future studies. I have also applied these techniques to study model systems, including ground states of the Bose-Hubbard model, high-temperature dynamics of the mass-imbalanced Fermi-Hubbard model, and phase transitions in the extended 2D Fermi-Hubbard model. To this end, I have implemented the VUMPS algorithm as well as a twist on the iTDVP algorithm using the ITensor library.

Relevant Article(s)

Superfluidity in the 1D Bose-Hubbard model, Thomas G. Kiely and Erich J. Mueller, Phys. Rev. B 105, 134502 (2022)

Role of conservation laws in the Density Matrix Renormalization Group, Thomas G. Kiely and Erich J. Mueller, Phys. Rev. B 106, 235126 (2022)

Bandwidth-tuned Wigner-Mott Transition at \(\nu=1/5\): an Infinite Matrix Product State Study, Thomas G. Kiely and Debanjan Chowdhury, preprint

High temperature Transport in the One Dimensional Mass-Imbalanced Fermi-Hubbard model, Thomas G. Kiely and Erich J. Mueller, in preparation