Quantum Phases of Matter

Questions

• How does the number of spatial dimensions alter the zero temperature (quantum) phase diagram? How does it change the nature of phase transitions?
  • Can superfluid phenomenology be observed in one-dimensional Luttinger liquids? If so, how can we measure it?
• What sorts of insulating phases are stabilized by long-range interactions?
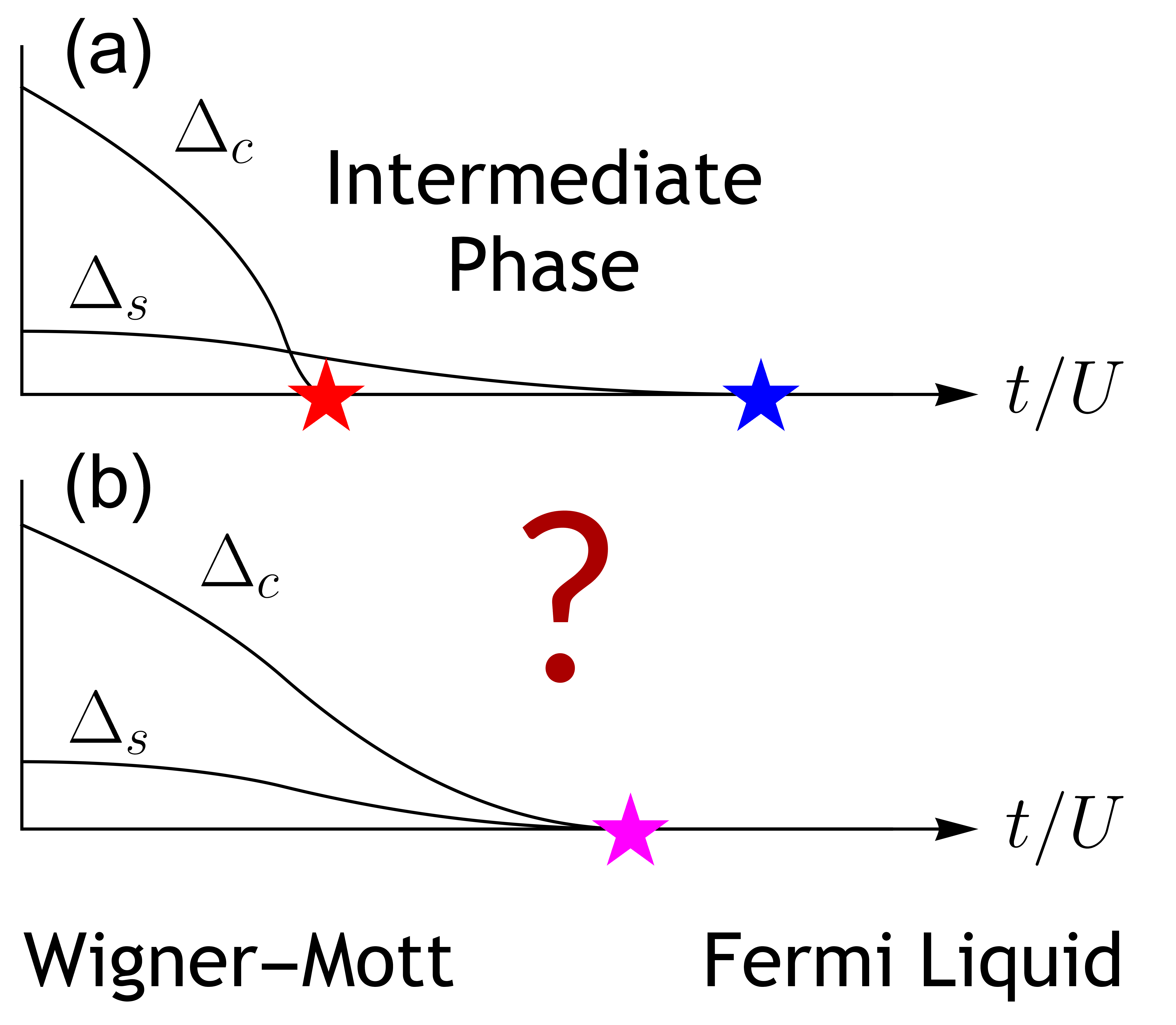
  • What is the nature of the Wigner-Mott metal-insulator transition in van der Waals heterostructures? Can similar physics be observed in Rydberg arrays?

Background

We’re all familiar with finite-temperature phase transitions: ice melting, water boiling, etc. In our everyday experience, these transitions are driven by changes in temperature, which simply the average kinetic energy of the system. When the temperature is very low, water molecules stick together and form a crystalline structure (ice). When the temperature is very high, the molecules spread out so that they can move around more easily. In this gaseous phase, those sticky interactions become less important. Interestingly, at an intermediate temperature scale the molecules form a liquid: they spread out enough to move around a bit, but interactions remain important.

In general, phase transitions depend on more than temperature. For example, the phase diagram of water depends also on the ambient pressure. In my work, I have thought about phase transitions that occur at zero temperature. In these systems, particles at zero temperature still have some finite kinetic energy due to quantum fluctuations. Hence, the phase transition depends on the ratio of those quantum fluctuations (which we refer to with an energy scale called the bandwidth) and the energy associated with interactions. Certain experimental systems, including cold atoms and van der Waals heterostructures, have demonstrated the ability to tune the ratio of bandwidth to interactions, hence allowing them to probe these transitions. While these experiments cannot reduce the temperature to zero, the effects of these zero-temperature critical points can still be seen at finite (albeit low) temperatures.

Relevant Article(s)

Superfluidity in the 1D Bose-Hubbard model, Thomas G. Kiely and Erich J. Mueller, Phys. Rev. B 105, 134502 (2022)

Bandwidth-tuned Wigner-Mott Transition at \(\nu=1/5\): an Infinite Matrix Product State Study, Thomas G. Kiely and Debanjan Chowdhury, preprint